Chapter 20 Multinomial Distribution
20.1 Chapter Scenario - 3D Ant Walking
Recall the ways can a person walk from corner X to another corner by a path of shortest length is \(\dbinom{n}{r}\) where n is the total number of blocks walked and r is the number of East blocks. If E is the number of blocks East and S is the blocks south then \(\dbinom{L+R}{L}\) or \(\dbinom{L+R}{R}\) nicely names the number of paths.
We now consider a similar three-dimensional structure called a lattice. How many ways are there for an ant to walk from one diagonal corner to the other in a path of shortest length for the situation pictured below?
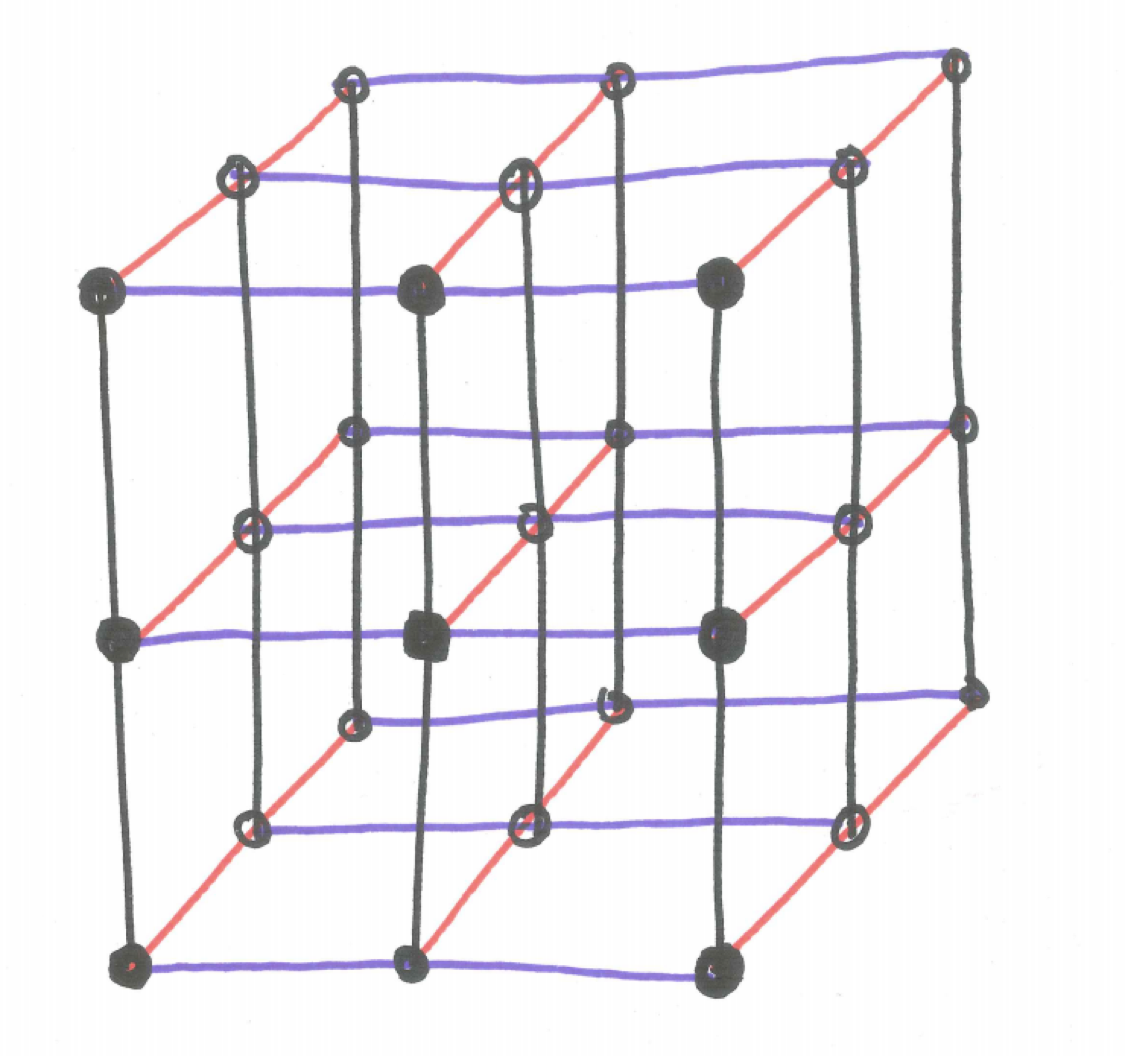
Figure 20.1: 3D Ant-walking Grid
20.2 Chapter Scenario Revisited - 3D Ant Walking
20.2.1 A Simpler Example
How many ways are there for an ant to walk from one diagonal corner to the other in a path of shortest length for the simpler situation pictured below?
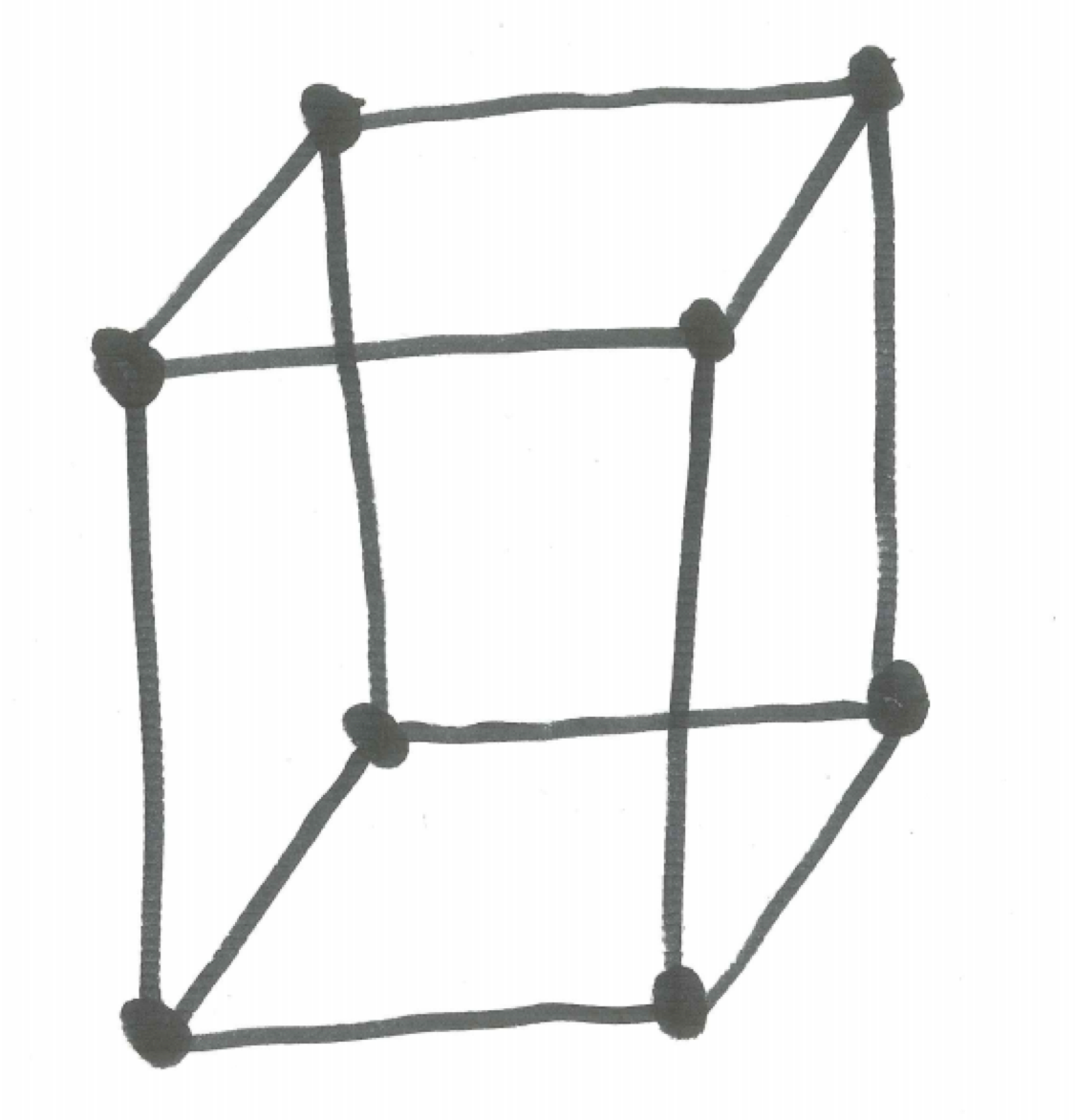
Figure 20.2: Simpler Ant-walking Grid
The example is small enough we could illustrate the solutions. Turns out there are six of them.
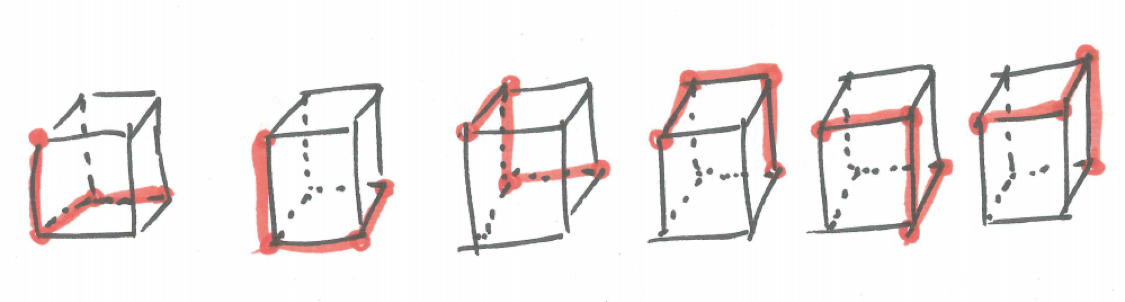
Figure 20.3: Simpler Ant-walking Grid Solutions
We can translate this ant-walking problem into a different context by labeling the directions the ant may walk. In addition to moving Left (L) or Right (R) the ant may travel Down (D).
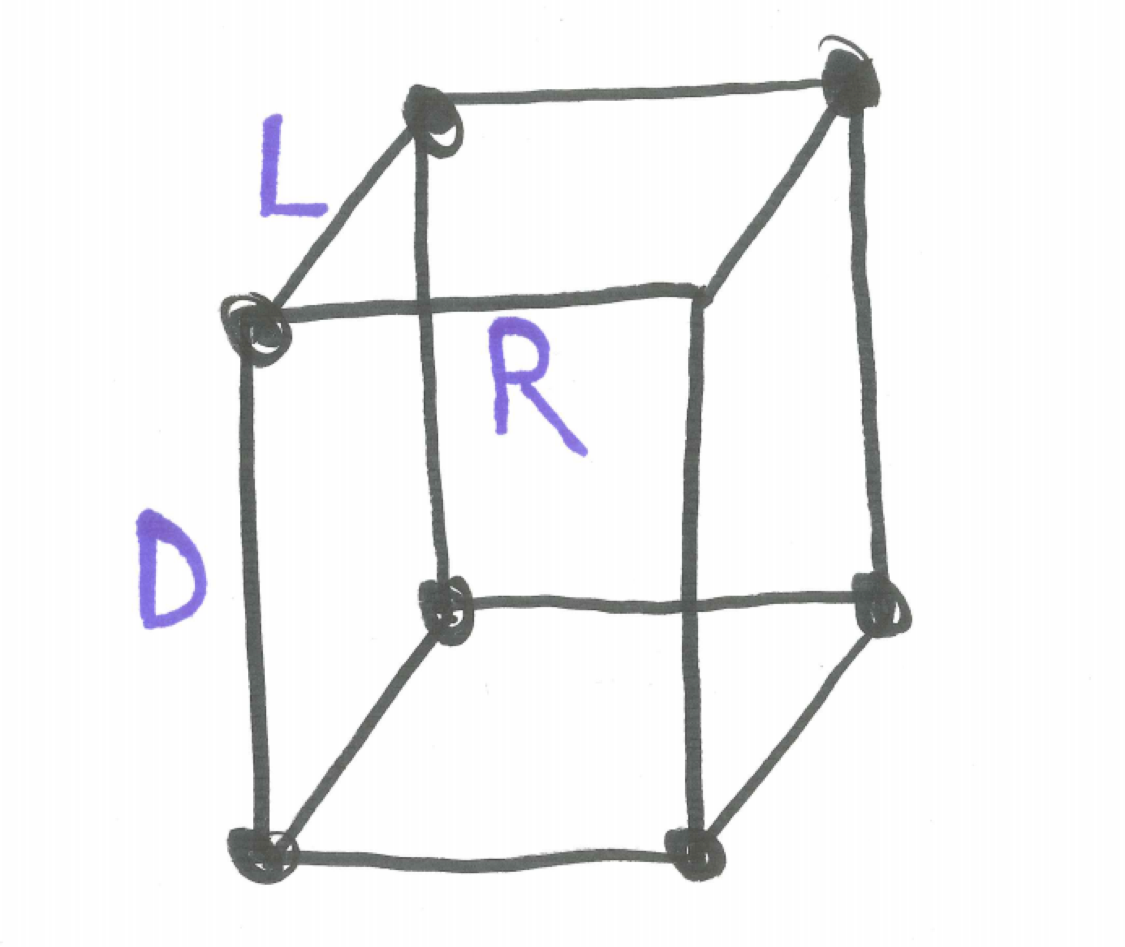
Figure 20.4: Simpler Ant-walking Grid with Labels
In moving from the top corner to the diagonally opposite bottom corner we recognize the ant make make one Left move, one Right move, and one Down move and the different paths can be described as the different orderings of one L, one R, and one D as written below.
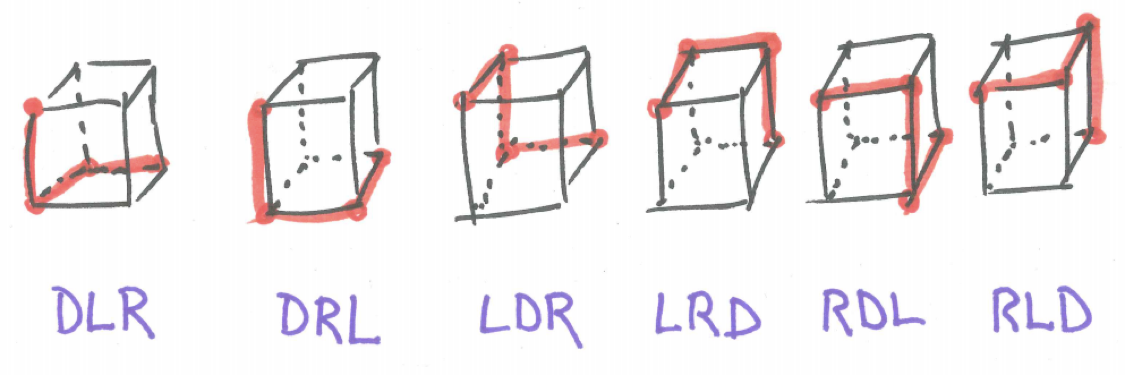
Figure 20.5: Simpler Ant-walking Grid Solutions with Orderings
20.2.2 The Original Problem
In the 2 x 2 x 2 grid the ant must travel two blocks to the left, two to the right, and two down. A particular path can be represented as a sequence of two L’s, two R’s, and two D’s. This can be done a total of \(\frac{6!}{2! \cdot 2! \cdot 2!}\) ways.
20.2.3 General 3D Lattice Situation
We may describe the general situation in a 3-D lattice with width W units, length L units, and height H units. How many paths are there from one corner to the diagonally opposite corner? This would be equivalent to the number of orderings of so many W’s, L’s, and H’s resulting in \(\frac{(W+L+H)!}{W! \cdot L! \cdot H!}\) unique paths.
20.3 Example - Hair Color
According to one source, \(84\%\) of the world has black hair, \(11\%\) has brown hair, \(3\%\) has blond hair, and \(2\%\) has red hair. Of course, various combinations of these account for more descriptive names - strawberry blond, etc. Suppose 50 individuals were selected at random. Because the human population of the earth is so large and our sample so small, we could use an urn model with replacement to help us think about this probability experiment. Consider an urn with \(84\%\) black beads, \(11\%\) brown beads, \(3\%\) blond beads, and \(2\%\) red beads. Draw 50 beads at random from this urn with replacement.
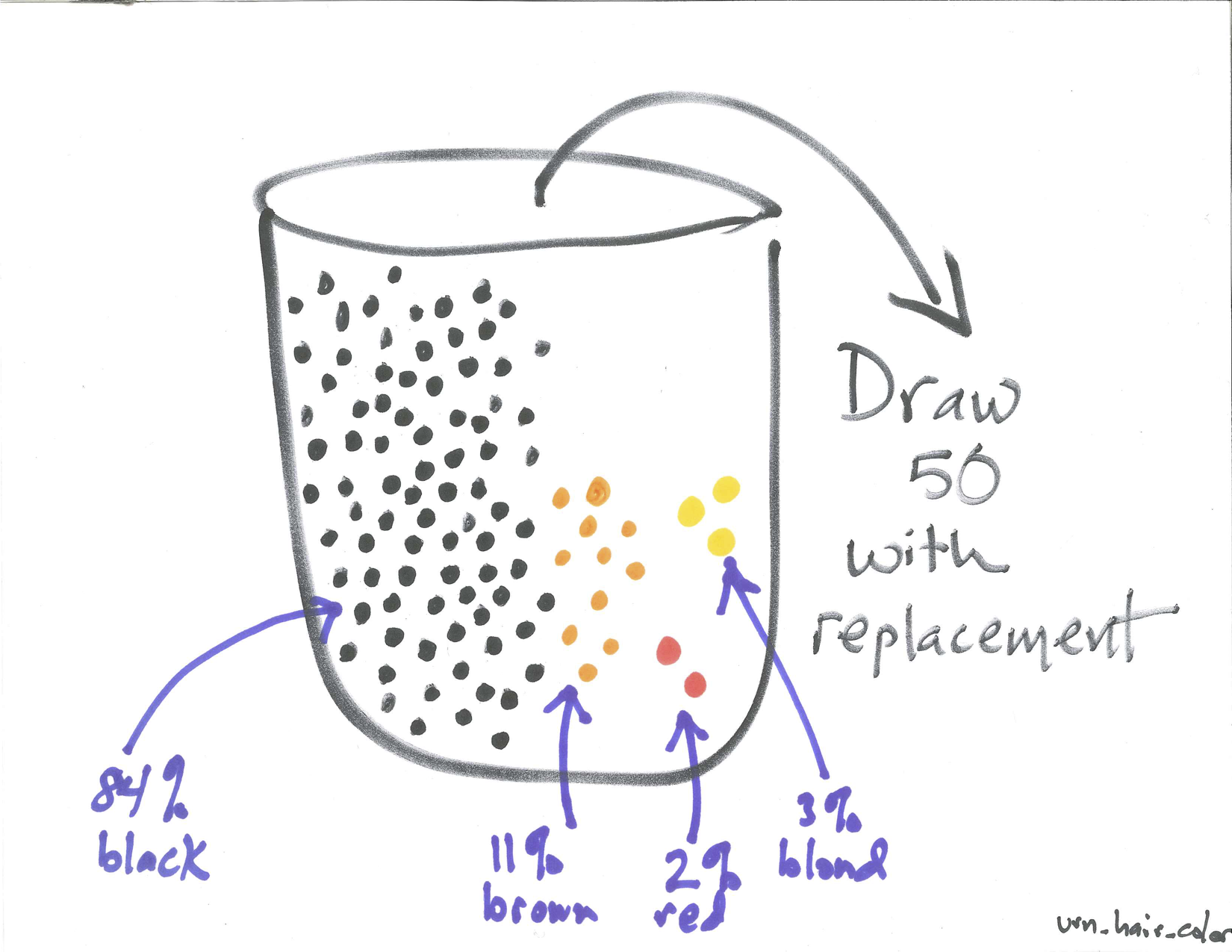
Figure 20.6: Urn Model for Hair Color
The distribution of hair color would have a multinomial probability distribution.
Source: https://infogram.com/most-common-hair-color-1gjk92e414wvp16